但由于宏观环境的不确定性,其在经济展望中上调了未来纪念通胀和失业率预测,并下调...

嘉盛FOREX提供最新股票交易服務,嘉盛集团证券投資平台覆蓋450多種全球股票及場差价合约產品。FOREX嘉盛集团官網接通全球企業場外股票交易,覆蓋全球資本市場上的知名公司,為投資者量身定制。




每周5天,每天24小时,交易超过80多个货币对
享受现货黄金产品为您带来优势,包括尽可能充足的流动性和极具竞争力的点差
交易全球股指,享受场外交易时间带来的便利
无论上涨或是下跌均可交易,双向把握潜在交易机会
交易4500多种全球场外股票,包括最受欢迎的中概股、蓝筹股等



在上千个市场中选择,在屡获殊荣的交易平台交易,享受金融巨头带来的安全感。作为纳斯达克上市金融巨头StoneX 集团的一部分,嘉盛为您提供独一无二的报价来源。
选择正规监管和财务稳健的交易提供商为交易带来安全感。
我们对低差点和清晰透明的报价引以为傲。在嘉盛,您将一直处于透明的环境。
嘉盛为您提供多种账户类型, 仅需几分钟,便可以完成填表注册,打开交易世界的大门。

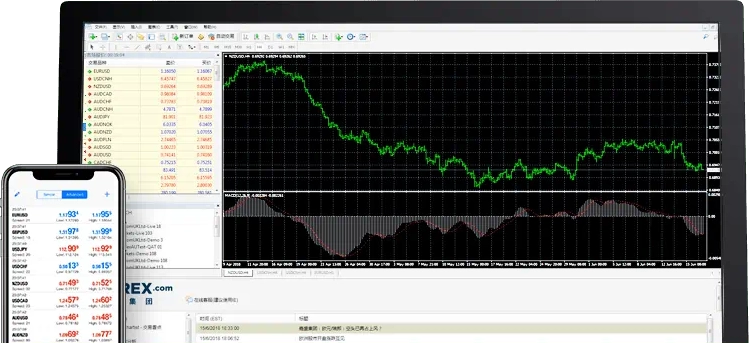
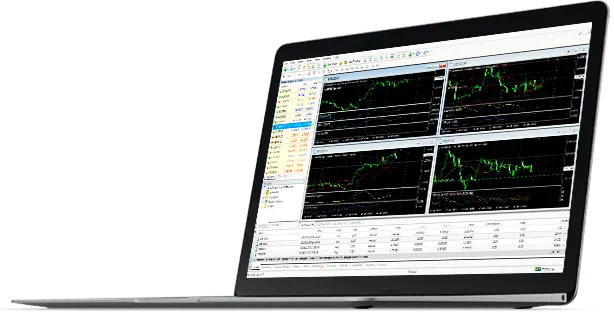
嘉盛最先进、最优化的MetaTrader平台


.png)
MT4交易平台 世界上最受欢迎的交易平台之一,并获得嘉盛集团的独家支持和整合
屡获殊荣的平台,兼容所有浏览器,日常交易的理想选择



但由于宏观环境的不确定性,其在经济展望中上调了未来纪念通胀和失业率预测,并下调...

尽管以色列和伊朗的军事冲突还在升级,但有关美国可能促成双方停火的消息还是提振了...

而本周包括美联储在内的众多央行决议或将给市场带来更大的波动。 上周市场回顾 中...

风险警示: 交易外汇和杠杆化金融品种具有高风险,可能导致您损失本金。您所承担的亏损风险不应超过您的承受能力,请确保您完全理解其中所涉风险。交易杠杆化产品并不适合所有投资者。在交易前,请考虑您的经验水平、投资目标,如有必要请寻求独立财务建议。客户有责任确保他/她所居住国法律要求允许其使用嘉盛外汇品牌提供的服务。
© 2022 digecoly All Rights Reserved by Dream-IT